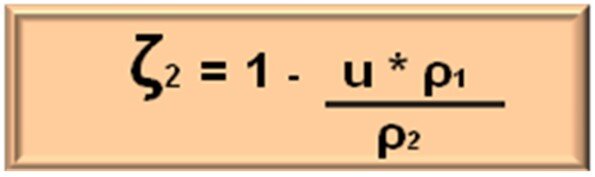Dank der sogenannte Libration können wir mehr als 50 % der Mondoberfläche sehen. Der Mond weist eine gebundene Rotation auf. Das heisst während eines Umlaufes um die Erde dreht sich der Mond einmal um sich selbst. Das war nicht immer so, in der Früh Phase unseres Mondes vor ca 4 Milliarden Jahren betrug das Verhältnis Umlaufzeit zu Rotation 2:3. Auf zwei Erdrotationen kamen drei Mondumrundungen. Durch gravitative Einflüsse änderten sich Rotationszeiten und Umlaufzeiten sowie Entfernung der beiden Himmelskörper. Dieser Vorgang dauerte einige hundert Millionen Jahre. Dieser Prozess ist allerdings noch immer am laufen und wird damit enden das die Erde 40 oder 50 Stunden braucht um eine Rotation zu vollführen und der Mond ins Sonnensystem weg driftet.
SPEKTRAL ANALYSE / SPECTRAL ANALYSIS
Im Jahre 1802 entdeckte der britische Chemiker William Hyde Wollaston als erster sogenannte Spektrallinien (Absorbtionslinien) im Licht der Sonne. Unabhängig davon und ca. 12 Jahre später entdeckte auch Joseph Fraunhofer dieses Phänomen und veröffentlichte seine Entdeckung. Als Spektrallinien bezeichnet man voneinander scharf getrennte Linien eines Spektrums emittierter oder absorbierter elektromagnetischer Wellen des sichtbaren Lichts. Früh erkannte man auch das jedes chemische Element sein ganz individuelles “Spektrum” besass. Dem Schweden Jonas Angström gelang es als erstem präzise die Wellenlänge der Emissions-Linien des Wasserstoffspektrums zu messen. Im sichtbaren Spektrum des Wasserstoffs sind sechs Emissions-Linien zu erkennen.
In 1802, the British chemist William Hyde Wollaston was the first to discover so-called spectral lines (absorption lines) in the light of the sun. Independently of this and about 12 years later, Joseph Fraunhofer also discovered this phenomenon and published his discovery. Spectral lines are sharply separated lines of a spectrum of emitted or absorbed electromagnetic waves of visible light. Early on, it was also recognized that each chemical element had its own individual "spectrum". The Swede Jonas Angström was the first to precisely measure the wavelength of the emission lines of the hydrogen spectrum. Six emission lines can be seen in the visible spectrum of hydrogen.
Man nennt diese Linien H-Linien (H=Hydrogenium) von links nach rechts Hα, Hβ, Hγ, Hδ, Hε und Hζ.
These lines are called H-lines (H=Hydrogenium) from left to right Hα, Hβ, Hγ, Hδ, Hε and Hζ.
Eine Emissions-Linie zeigt sich im Spektrum als helle Linie. Sie entsteht beim Übergang von einem höheren auf ein tieferes Energieniveau, beispielsweise wenn ein Elektron von einem angeregten Zustand in den Grundzustand übergeht. Hierbei wird ein Photon ausgesendet. Im Gegensatz dazu zeigt eine Absorption von Photonen eine dunkle Linie im Spektrum des jeweiligen Chemischen Elementes. Man spricht hier von Absorbtions-Linien.
An emission line appears in the spectrum as a bright line. It occurs during the transition from a higher to a lower energy level, for example when an electron passes from an excited state to the ground state. A photon is emitted. In contrast, an absorption of photons shows a dark line in the spectrum of the respective chemical element. This is called absorption lines.
Emissionslinien entstehen wenn Elektronen von einem höheren auf ein tieferes Energieniveau fallen und emittieren deshalb Photonen.
Emission lines are formed when electrons fall from a higher to a lower energy level and therefore emit photons.
Absorbtionslinien entstehen wenn Elektronen von einem tieferen auf ein höheres Energieniveau gelangen und absorbieren deshalb Photonen.
Absorption lines are formed when electrons travel from a lower to a higher energy level and therefore absorb photons.
Elektronen eines chemischen Elementes halten sich in Energieorbitalen auf. Ein Orbital ist eine räumliche Wellenfunktion die aussagt mit welcher Wahrscheinlichkeit ein Elektron an einem bestimmten Ort im Orbital anzutreffen ist. Elektronen können in diesen Orbitalen hin und her wechseln sobald Energie zu oder abgeführt wird. Die Sprünge sind allerdings Diskret, das heisst es können nicht beliebige Energiestufen erreicht werden. Die Messungen von Angström zeigen Emissionslinien deren Energieniveau in der L-Schale also dem zweituntersten Energiezustand der Elektronen entsprechen.
Electrons of a chemical element reside in energy orbitals. An orbital is a spatial wave function that indicates the probability of an electron at a certain location in the orbital. Electrons can switch back and forth in these orbitals as soon as energy is supplied or dissipated. However, the jumps are discrete, which means that not arbitrary energy levels can be achieved. The measurements of Angström show emission lines whose energy level in the L-shell corresponds to the second lowest energy state of the electrons.
Die Linie H-η (H-Eta) ganz rechts liegt bereits im unsichtbaren Bereich des Spektrums. (Ultraviolett)
The line H-η (H-Eta) on the far right is already in the invisible area of the spectrum. (Ultraviolet)
Genau hier bringt im Jahre 1885 ein Schweizer Mathematiker namens Johann Jakob Balmer die Messreihe von Jonas Angström aufs Tapet. Wahrscheinlich eher durch Zufall erfuhr vom Basler Physikprofessors Eduard Hagenbach-Bischoff in einer Vorlesung von der Messreihe Angströms. Die Zahlenreihe erweckte die Neugier in Ihm und so begann er an Ihnen herum zu manipulieren. Er entdeckte das sich die Verhältnisse der Wellenlänge durch Verhältnisse kleiner Zahlen in Bruchform darstellen lassen.
This is exactly where a Swiss mathematician named Johann Jakob Balmer brings Jonas Angström's series of measurements to the table in 1885. Probably by chance, the Basel physics professor Eduard Hagenbach-Bischoff learned about Angström's series of measurements in a lecture. The series of numbers aroused curiosity in Him and so He began to manipulate you. He discovered that the ratios of the wavelength can be represented by ratios of small numbers in fractional form.
Das Verhältnis 8 : 5 = 1.6 bildet das Verhältnis 656.2792 : 410.1738 = 1.600002974 fast perfekt ab. Balmer wusste natürlich über die Messfehler solcher Experimente in der Physik.
The ratio 8 : 5 = 1.6 represents the ratio 656.2792 : 410.1738 = 1.600002974 almost perfectly. Balmer, of course, knew about the measurement errors of such experiments in physics.
Johann Balmer spürte förmlich die Gesetzmässigkeit dieser Tatsachen und suchte nach einem gemeinsamen Faktor k mit dem sich die Wellenlänge aller Emissions-Linien des Wasserstoffs berechnen liessen. Den Faktor fand er durch probieren und ständigem Anpassen mit
Johann Balmer formally sensed the laws of these facts and was looking for a common factor k with which the wavelength of all emission lines of hydrogen could be calculated. He found the factor by trying and constantly adapting with
Nun musste er für die entsprechenden Wellenlängen der einzelnen Linien geeignete Brüche finden die mit dem Faktor k multipliziert die entsprechende Wellenlänge ergaben.
Now he had to find suitable fractions for the corresponding wavelengths of the individual lines, which multiplied by the factor k resulted in the corresponding wavelength.
Auf den ersten Blick scheint es so als ob diese Brüche eher dem Zufall entsprungen sind da kein offensichtliches Bildungsgesetz zu erkennen ist. Wird aber der Hβ Bruch mit vier erweitert so erhalten wir
At first sight, it seems as if these fractions are rather by chance because there is no obvious mathematical law to recognize. But if the Hβ fraction is extended with four, we get
und jetzt wird das Bildungsgesetz offensichtlich. Im Zähler des Bruches sind Quadratzahlen von n (n=>3) und im Nenner die Quadratzahl des Zählers um vier vermindert.
and now the mathematical law is becoming obvious. In the numerator of the fraction square numbers of n (n=>3) and in the denominator the square number of the numerator are reduced by four.
Somit lässt sich dieses Bildungsgesetz mittels obiger Formel darstellen. Jakob Balmer entdeckte das Bildungsgesetz durch probieren und dem Glück des tüchtigen. Die Physiker, allen voran Niels Bohr und Paul Dirac wussten aber, das da viel mehr als nur eine Formel dahintersteckte, nämlich der Beginn der Quantenphysik . Mit der Balmer-Formel lassen sich alle Spektrallinien des Wasserstoffs berechnen deren Elektronen in die L-Schale “zurückfallen”. Jedoch gibt es auch Elektronen die zuvor angeregt wurden und in andere Schalen des Orbitals zurückfallen. Diese Linien konnten erst durch die Erweiterung von Johannes Rydberg berechnet werden, der die Balmer-Formel umformte. Man spricht hier von der Rydberg-Formel oder der Rydberg Erweiterung.
Thus, this education law can be represented by means of the above formula. Jakob Balmer discovered the education law through trial and error and the happiness of the capable. However, the physicists, above all Niels Bohr and Paul Dirac, knew that there was much more than just a formula behind it. With the Balmer formula, all spectral lines of hydrogen can be calculated whose electrons "fall back" into the L-shell. However, there are also electrons that were previously excited and fall back into other shells of the orbital. These lines could only be calculated by the extension of Johannes Rydberg, who reshaped the Balmer formula. This is referred to as the Rydberg formula or the Rydberg extension.
TELESKOPE / TELESCOPES
Allgemeines
Die Erforschung des Weltalls wurde erst mit der Erfindung des Fernrohres oder Teleskopes möglich. Die Leistung eines Teleskopes wird durch den Linsen Ø oder den Spiegel Ø bestimmt. Bei einer Verdoppelung des Linsen oder Spiegeldurchmessers steigt die Auflösung eines Teleskopes ebenfalls um das doppelte an, die Lichtsammelwirkung sogar um das Vierfache. Die Vergrösserung eines Teleskopes hingegen sagt nichts über die Leistung aus. Mit entsprechenden kurzbrennweitigen Okularen kann fast jede beliebige Vergrösserung erzielt werden. Das Bild jedoch, wird dadurch immer Dunkler und Kontrastloser je mehr man vergrössert.
The exploration of space only became possible with the invention of the telescope. The power of a telescope is determined by the lenses Ø or the mirror Ø. With a doubling of the lens or mirror diameter, the resolution of a telescope also increases by twice, the light-collecting effect even by four times. The magnification of a telescope, on the other hand, says nothing about the performance. With corresponding short focal length eyepieces, almost any enlargement can be achieved. However, the image becomes darker and darker and less contrast the more you enlarge.
Linsenteleskope (Refraktoren)
Linsenteleskope (Refraktoren), bestehen aus verschiedenen Linsen, die durch entsprechende Kombination eine lichtsammelnde Wirkung erzeugen. Diese Linsen erzeugen in der Brennebene ein seitenverkehrtes und auf dem Kopf stehendes Bild das im Okular betrachtet werden kann. Wir unterscheiden zwischen Sammellinsen und Zerstreuungslinsen.
Lens telescopes (Refractors) consist of different lenses, which produce a light-collecting effect by appropriate combination. These lenses produce a side-side and upside-down image in the focal plane that can be viewed in the eyepiece. We distinguish between collecting lenses and scattering lenses.
Bei Sammellinsen wird Parallel einfallendes Licht wird in ihrer Brennebene gesammelt. Speziell wird parallel zur optischen Achse eingestrahltes Licht im Brennpunkt fokussiert.
Die Streuungslinse fokussiert parallel einfallendes Licht nicht, sondern zerstreut es, wenn es durch die Linse gebrochen wird. Man nennt Streuungslinsen auch Negativlinsen, weil der Brennpunkt der Lichtstrahlen vor der Linse liegt.
Lichtstrahlen werden von einer Linse beim Eintritt in den Linsenkörper abgelenkt (abhängig vom Radius R1) und beim Austritt ein zweites mal (abhängig vom Radius R2). Die abgelenkten Strahlen schneiden sich im Fokuspunkt.
Light rays are deflected by a lens when entering the lens body (depending on radius R1) and at exit a second time (depending on radius R2). The deflected rays intersect in the focal point.
Wesentlich für die Berechnung von Linsen sind die Krümmungsradien R1 und R2, die Dicke der Linse d und der Brechungsindex n des verwendeten Materials. Daraus ergibt sich die Brennweite f und demzufolge der Fokuspunkt.
Für ein einfaches Linsenteleskop genügen im Prinzip zwei Linsen. Die Sammellinse in der das eintreffende Licht gebrochen in den Fokuspunkt weitergeleitet wird und das Okular indem der Betrachter das Bild sichtbar machen kann. Die ersten Teleskope waren Linsenfernrohre die um 1608 von einem holländische Optiker (Hans Lipperhey) entwickelt wurden. Die Technik wurde von Galileo Galilei weiterentwickelt. Er kombinierte eine Sammellinse und eine Zerstreuungslinse (Okular) derart, das eine Seitenrichtiges und Aufrechtstehendes Bild entstand.
In principle, two lenses are sufficient for a simple lens telescope. The collection lens in which the incoming light is broken is passed into the focus point and the eyepiece by the viewer can make the image visible. The first telescopes were lens telescopes developed around 1608 by a Dutch optician (Hans Lipperhey). The technology was further developed by Galileo Galilei. He combined a collecting lens and a scattering lens (eyepiece) in such a way that a side-correct and upright image was created.
Prinzipdarstellung eines Linsenteleskopes. Das Okular kann entlang der optischen Achse so verstellt werden, dass sich die Brennpunkte von Linse und Okular vereinen.
Jedoch haben einfache Linsenteleskope einen gravierenden Fehler. Beim eintreten des Lichtes in eine Sammellinse wirkt diese wie ein Prisma. Das weisse Licht wird in seine Bestandteile Rot, Grün und Blau zerlegt. Da die unterschiedlichen Farben durch unterschiedliche Wellenlängen entstehen, treffen die einzelnen Farben nicht in einem gemeinsamen Fokuspunkt zusammen. Dieses Phänomen wird als “Chromatische Aberration” bezeichnet. Bilder mit chromatischer Aberration weisen Farbfehler auf und sind aufgrund der unterschiedlichen Fokuspunkte nicht scharf.
However, simple lens telescopes have a serious flaw. When the light enters a collection lens, it acts like a prism. The white light is broken down into its components red, green and blue. Because the different colors are created by different wavelengths, the individual colors do not meet in a common focus point. This phenomenon is called "chromatic aberration". Images with chromatic aberration have color errors and are not sharp due to the different focus points.
Der Chromat
Beim eintreten des Lichtes in eine Sammellinse wirkt diese wie ein Prisma. Das weisse Licht wird in seine Bestandteile Rot, Grün und Blau zerlegt. Da die unterschiedlichen Farben durch unterschiedliche Wellenlängen entstehen, treffen die einzelnen Farben nicht in einem gemeinsamen Fokuspunkt zusammen. Dieses Phänomen wird als “Chromatische Aberration” bezeichnet.
Linsenteleskope mit nur einer Linse werden als “Chromaten” bezeichnet. Um den gravierenden Nachteil der Chromatischen Aberration zu eliminieren, entwickelte der Engländer Chester Moore Hall um 1733 sogenannte “Achromaten”. Diese Linsenteleskope besitzen zwei Sammellinsen, die einen unterschiedlichen Brechungsindex besitzen. Das Flintglas mit einem hohen Anteil an Bleioxid besitzt einen Abbe-Wert von < 50, beim Kronglas ist er > 50. Dies bewirkt das Blaues Licht in den Fokuspunkt des Roten Lichts verschoben wird, der Abbildungsfehler wird reduziert. Die Konstruktion solcher achromatischer Linsensysteme beruht darauf, dass das Verhältnis von Brechungsindex und Dispersion für verschiedene Glassorten unterschiedlich ist.
Lens telescopes with only one lens are called "chromates". In order to eliminate the serious disadvantage of chromatic aberration, the Englishman Chester Moore Hall developed so-called "achromats" around 1733. These lens telescopes have two collection lenses that have a different refractive index. The Flint glass with a high content of lead oxide has an abbe value of < 50, with the crown glass it is > 50. This causes the blue light to be moved to the focus point of the red light, the imaging error is reduced. The design of such achromatic lens systems is based on the fact that the ratio of refractive index and dispersion is different for different types of glass.
Der Achromat
Beim Austritt des Lichts aus der Bikonvexen Linse wird das Blaulicht von der Plankonkaven Linse unter einem andren Winkel abgelenkt. Der Fokuspunkt von Rot und Blaulicht fallen zusammen, dies führt zu einer Minimierung des Abbildungsfehlers.
Um den Abbildungsfehler nochmals zu Minimieren musste das Linsenteleskop erneut verbessert werden. Dies gelang dem Briten Peter Dollond 1765 durch den Einbau einer dritten Linse. Bei den sogenannten Apochromaten muss darauf geachtet werden, dass die Glaswerkstoffe entsprechend ihrem Brechungsindex kombiniert werden.
In order to minimize the imaging error, the lens telescope had to be improved again. The British Peter Dollond succeeded in this in 1765 by installing a third lens. In the case of so-called Apochromates, care must be taken to ensure that the glass materials are combined according to their refractive index.
Der Apochromat
Refraktoren mit drei Linsen werden Apochromaten genannt. Ein Apochromat weist fast gar keine Chromatische Aberration mehr auf. Jedoch muss auch berücksichtigt werden das jede zusätzliche Linse unweigerlich zu Informationsverlust infolge Absorption im Linsenkörper führt.
Die Leistung eines Teleskopes ist vom Durchmesser der Linse abhängig. Verdoppelt man den Ø einer Linse, verdoppelt man auch die Auflösung. Die lichtsammelnde Wirkung steigt sogar Quadratisch mit der Verdoppelung des Durchmessers an. Jedoch waren der Grösse der Linsen im 17. Jahrhundert Grenzen gesetzt. Das Problem war die Herstellung der Glasblöcke aus denen die Linsen geschliffen wurden. Das Glas durfte keinerlei Einschlüsse aufweisen. Um 1785 gelang es dem Schweizer Pierre Louis Guinand als erstem (noch vor Fraunhofer) absolut homogene Glasblöcke herzustellen.
The power of a telescope depends on the diameter of the lens. If you double the size of a lens, you also double the resolution. The light-collecting effect even increases squarely with the doubling of the diameter. However, the size of the lenses was limited in the 17th century. The problem was the production of the glass blocks from which the lenses were sanded. The glass was not allowed to show any inclusions. Around 1785, the Swiss Pierre Louis Guinand was the first (before Fraunhofer) to produce absolutely homogeneous glass blocks.
Pierre Louis Guinand wurde am 20. April 1748 in La Corbatiere geboren und Verstarb am 13. Februar 1824 in Brenets. Er war gelernter Optiker und Unternehmer und führte mit seinen Söhnen eine Fabrik zur Glasherstellung. Mit seiner entwickelten Technologie war es möglich Glaslinsen höchster Reinheit herzustellen. Er leitete die berühmte Linsenmanufaktur von “Benediktbeuren” im heutigen Bayern bevor er von Joseph Fraunhofer verdrängt wurde.
Mit seinem Verfahren dem “Guinandage” konnte er den Linsenrohling mittels einem zylindrischen Ton-stab homogenisieren und somit ohne Blasen und Schlieren herstellen. Vor Guinand betrug der maximale Linsendurchmesser 10 cm. Dank seiner Technologie wurden bald Linsen mit einem Durchmesser von bis zu 60 cm und mehr hergestellt. In der Folge wurden immer grössere Linsen und somit Leistungsfähigere Teleskope gebaut.
With his "Guinandage" method, he was able to homogenize the lens blank using a cylindrical clay rod and thus produce it without blisters and streaks. Before Guinand, the maximum lens diameter was 10 cm. Thanks to its technology, lenses with a diameter of up to 60 cm and more were soon produced. As a result, ever larger lenses and thus more powerful telescopes were built.
Im 19. Jahrhundert war der Besitz des grössten Teleskopes eine Image-Angelegenheit. Rekorde wurden fast jährlich gebrochen. Der Höhepunkt wurde 1897 mit dem Grossen Refraktor von George Willis Ritchey erreicht. Seine Linse hat einen Durchmesser von 1020 mm und eine Brennweite von 19.79 Metern.
In the 19th century, the ownership of the largest telescope was an image affair. Records were broken almost every year. The climax was reached in 1897 with the Great Refractor by George Willis Ritchey. Its lens has a diameter of 1020 mm and a focal length of 19.79 meters.
Die Grenzen des technisch machbaren waren erreicht. Durch die enorme Grösse der Linse biegt sie sich durch und verursacht Verzerrungen. Infolge der Dicke des Glaskörpers wird Zuviel Licht absorbiert und schlussendlich erfordert die Montierung eine stabile Konstruktion damit keine Erschütterungen auftreten.
The limits of what is technically feasible had been reached. Due to the enormous size of the lens, it bends through and causes distortions. Due to the thickness of the vitreous, too much light is absorbed and finally the mounting requires a stable construction so that no vibrations occur.
The Big Refractor…………. at Yerkes Observatory Wisconsin USA.
Spiegelteleskope (Reflektoren)
Ein Spiegelteleskop besteht aus zwei Spiegeln, dem Primärspiegel und dem Sekundärspiegel. Das eintretende Licht wird vom Primärspiegel (Hohlspiegel) auf den Sekundärspiegel fokussiert und dieser fokussiert in eine Okularlinse. Im Gegensatz zu einem Linsenteleskop wird das Licht nicht gebrochen sondern reflektiert. Dadurch wird die Chromatische Aberration vermieden. Man unterscheidet Sphärisch und Parabolisch geschliffene Spiegel.
A reflector telescope consists of two mirrors, the primary mirror and the secondary mirror. The entering light is focused by the primary mirror (concave mirror) on the secondary mirror and this focuses into an eyepiece lens. In contrast to a lens telescope, the light is not refracted but reflected. This avoids chromatic aberration. A distinction is made between spherical and parabolic ground mirrors.
Die Parabel entsteht aus der Funktion Y = X²
Die Kreis Gleichung r² = X² + Y²
Spiegelsegmente aus Kreis und Parabel.
Selbstverständlich bestehen die Spiegel nur aus einem Segment der Parabel oder des Kreises. Spiegelteleskope gibt es in den verschiedensten Konstruktionsarten. Das Spiegel zu Beobachtungszwecken verwendet werden können ist schon seit dem 13. Jahrhundert bekannt. Der Jesuitenpater und Astronom Nicolaus Zucchius gilt als Erbauer des erste richtigen Spiegelteleskopes im Jahre 1616. Jedoch hatte sein Teleskop durch den leicht gekippten Spiegel riesige Abbildungsfehler. Issac Newton verbesserte die Konstruktion entscheidend indem er einen 45° Umlenkspiegel einbrachte, der das Licht aus der optischen Achse seitlich umlenkte und in ein Okular leitete.
Of course, the mirrors consist of only one segment of the parabola or circle. Reflector telescopes are available in a wide variety of construction types. The mirror can be used for observation purposes has been known since the 13th century. The Jesuit priest and astronomer Nicolaus Zucchius is considered the builder of the first real reflecting telescope in 1616. However, his telescope had huge imaging errors due to the slightly tilted mirror. Issac Newton significantly improved the design by introducing a 45° deflection mirror that deflected the light from the optical axis laterally and directed it into an eyepiece.
Das Newton Spiegelteleskop
Newton verwendete eine konkaven sphärischen Spiegel aus Spiegelmetall (CuSnZn). Das einfallende Licht wurde vom Primärspiegel auf einen Sekundärspiegel umgeleitet und seitlich in ein Okular abgelenkt.
Um 1672 entwickelte der französische Geistliche Laurent Cassegrain ein Spiegelteleskop mit einem durchbohrten Sekundärspiegel. Die brachte entscheidende Vorteile. Auf der einen Seite wurde die Spiegelmontierung wie bei Newton noch üblich eliminiert. Der Sekundärspiegel wird auf einer Glasscheibe untergebracht. Auf der anderen Seite wurde der Sekundärspiegel so angeordnet, dass die Fokussierung der Lichtstrahlen vom Primärspiegel hinter dem Sekundärspiegel stattfindet. Dies führt zu einer extrem kurzen Bauweise der Teleskope.
Around 1672, the French clergyman Laurent Cassegrain developed a reflecting telescope with a pierced secondary mirror. This brought decisive advantages. On the one hand, the mirror mount was eliminated as usual with Newton. The secondary mirror is housed on a glass pane. On the other hand, the secondary mirror has been arranged in such a way that the focusing of the light rays from the primary mirror takes place behind the secondary mirror. This leads to an extremely short design of the telescopes.
Das Cassegrain Spiegelteleskop
Das Licht wird von einem konkav-parabolischen Primärspiegel auf einen konvex-hyperbolischen Sekundärspiegel reflektiert und danach durch den Primärspiegel hindurch zum Okular. Cassegrain Teleskope weisen aufgrund der Spiegel eine relativ grosse Sphärische Aberration auf.
Im Laufe der Jahre wurden die Spiegelteleskope immer weiter verbessert. Heute gibt es die verschiedensten Typenkombinationen je nach Anwendung. Um die sphärische Aberration weitgehend zu eliminieren wurde das Cassegrain Teleskop mit einer sogenannten Schmidt-Platte versehen. Der asphärische Schliff dieser Linse erlaubt die Herstellung von nahezu “Koma” freier optischer Systeme.
Over the years, the reflector telescopes have been further improved. Today there are a variety of type combinations depending on the application. In order to largely eliminate spherical aberration, the Cassegrain telescope was provided with a so-called Schmidt plate. The aspherical cut of this lens allows the production of almost "coma free" optical systems.
Schmidt-Cassegrain Teleskop
Das Schmidt-Cassegrain Teleskop gehört zu den sogenannten Kata dioptrischen Teleskopen. Das Bild wird mittels Spiegeln und Linsen erzeugt. Die Schmidt-Platte (Blau) kompensiert die sphärische Aberration des Primärspiegels und ermöglicht eine fast Kommafreie Darstellung der Objekte.
Im Gegensatz zu den Refraktoren sind die Spiegelteleskope anfälliger was Erschütterungen anbelangt. Die Ausrichtung (Kollimation) der Primär und Sekundärspiegel sollte immer kontrolliert und gegebenenfalls korrigiert werden.
MONDBAHN / MOONORBIT
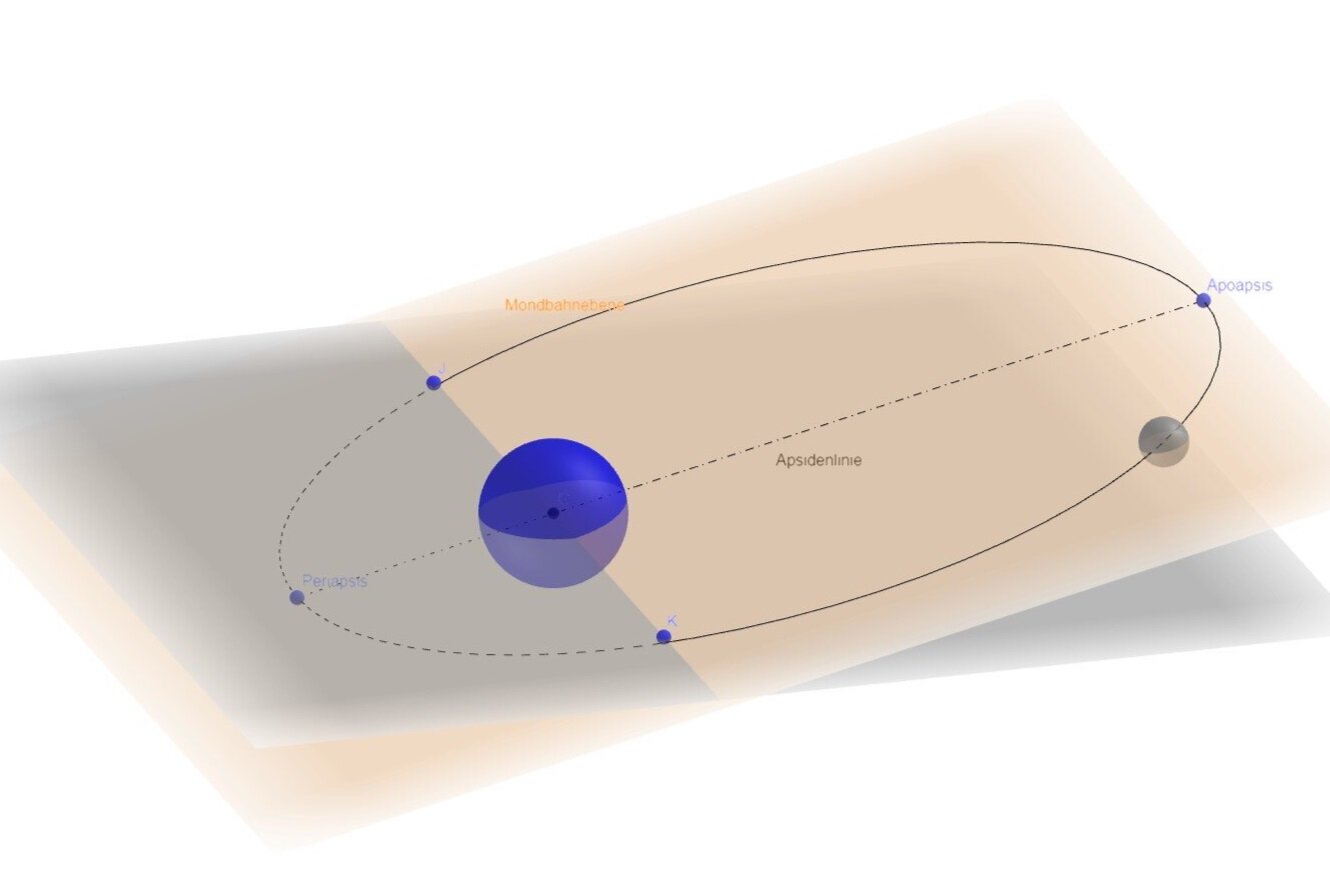
Die Umlaufbahn des Mondes um die Erde entspricht einer Ellipse mit einer numerischen Exzentrizität von 0.055545. Während in der Mathematik die Exzentrizität einer Ellipse mit der Distanz zwischen einem der beiden Brennpunkte (F1, F2) und dem Mittelpunkt M definiert ist (e = lineare Exzentrizität), gilt in der Astronomie für die Beschreibung eines Orbits die numerische Exzentrizität E. E ist definiert durch den Quotienten e/a, also lineare Exzentrizität dividiert durch die grosse Halbachse a. Die Exzentrizität beschreibt also die Abweichung einer Ellipse von einem Kreis.
The orbit of the moon around the Earth corresponds to an ellipse with a numerical eccentricity of 0.055545. While in mathematics the eccentricity of an ellipse is defined with the distance between one of the two focal points (F1, F2) and the center M (e = linear eccentricity), in astronomy the numerical eccentricity E. E is defined by the quotient E/a, i.e. linear eccentricity divided by the large half axis a. The eccentricity thus describes the deviation of an ellipse from a circle.
Mit einer numerischen Exzentrizität von 0.055545 beschreibt die Mondbahn fast eine Kreisbahn um die Erde, aber eben nur fast. In einem der beiden Brennpunkte (F1, F2) einer Ellipse befindet sich der Zentralkörper (Erde). Durch die Gravitationseinwirkung der Erde umkreist der Mond dieselbe. Das gemeinsame Rotationszentrum befindet sich nicht wie erwartet im Erdmittelpunkt, sondern im sogenannten Baryzentrum dem gemeinsamen Schwerpunkt ca. 1700 km unterhalb des sublunaren Punktes im Erdmantel.
With a numerical eccentricity of 0.055545, the lunar orbit describes almost a circular orbit around the Earth, but only almost. In one of the two focal points (F1, F2) of an ellipse is the central body (earth). Due to the gravitational effect of the Earth, the moon orbits the same. The common rotation center is not located in the center of the earth as expected, but in the so-called bary center of the common center of gravity about 1700 km below the sublunar point in the earth's mantle.
Da die Mondbahn eine Ellipse beschreibt, ist seine Distanz zur Erde variabel. Das Apogäum ist im Mittel 405`504 km von der Erde entfernt, das Perigäum im Mittel 363`296 km. Die Verbindung von Apogäum und Perigäum nennt man Apsidenlinie oder Apsis. Die Apoapsis ist also der Scheitel mit der grössten Entfernung und die Periapsis der Scheitel mit der kleinsten Entfernung zum Zentralkörper.
Since the lunar orbit describes an ellipse, its distance from Earth is variable. The Apogäum is on average 405'504 km from the earth, the perigee on average 363'296 km. The combination of apogee and perigee is called an apse line or apse. The apoapsis is thus the apex with the greatest distance and the periapsis of the apex with the smallest distance to the central body.
Die Apsiden erhalten unterschiedliche Bezeichnungen bezüglich ihres Zentralkörpers. So zum Beispiel
Sonne = Aphel und Perihel (hel = Helios die Sonne)
Erde = Apogäum und Perigäum (gäum = Gaia die Erde)
Mars = Apares und Periares (ares =Mars)
Die grau gefärbte Ebene markiert die Ekliptik, also die Ebene auf der die Erde die Sonne umkreist. Die braun eingefärbte Ebene, ist die Ebene der Mondbahn, sie ist im mittel 5.14527° gegenüber der Ekliptik geneigt. Die beiden Punkte J,K markieren die Stellen wo der Mond die Ekliptik ebene schneidet, die sogenannten Knoten (Drachenpunkte). Die Verbindung der beiden Punkte heisst Knotenlinie. Die Zeitdauer die der Mond benötigt um durch den gleichen Knoten zu wandern wird als “Drakonitischer Monat” bezeichnet und Dauert im mittel 27.212221 Tage. Mond oder Sonnenfinsternisse sind nur in der Nähe der beiden Knoten möglich und auch immer nur bei gleichzeitigem Vollmond oder Neumond. Die Knoten sind nicht fix im Raum sondern verschieben sich retrograd um ca. 19.3° pro Jahr.
The gray-colored plane marks the ecliptic, the plane on which the Earth orbits the sun. The brown colored plane, is the plane of the lunar orbit, it is inclined in the mean 5.14527° opposite the ecliptic. The two points J,K mark the places where the moon intersects the ecliptic plane, the so-called nodes (dragon points). The connection of the two points is called node line. The time it takes for the moon to travel through the same node is called the "Drakonite Month" and lasts in the middle of 27.212221 days. Moon or solar eclipses are only possible near the two knots and only at the same time full moon or new moon. The knots are not fixed in space but shift retrograde by about 19.3° per year.
Simulation in GEOGEBRA zur Berechnung der Drachenpunkte. Distanzen und Geschwindigkeiten entsprechen nicht der Realität.
Simulation in GEOGEBRA to calculate the dragon points. Distances and speeds do not correspond to reality.
Die meisten Grundlagen wurden bereits im 16. - 19. Jahrhundert erarbeitet. Anlässlich meines Besuches in der Sternwarte von Greenwich im Jahre 2016 war ich auf den Spuren der ersten “Himmelsmechaniker”. Es sind Namen wie Kepler, Kopernikus, Bradley, Newton und Halley die die Himmelsmechanik revolutionierten.
Most of the foundations were already worked out in the 16th - 19th century. On the occasion of my visit to the Greenwich Observatory in 2016, I was following in the footsteps of the first "heavenly mechanics". They are names like Kepler, Copernicus, Bradley, Newton and Halley that revolutionized celestial mechanics.
John Flamsteed geboren am 19. August 1646 Denby , Derbyshire und gestorben am 31. Dezember 1719 Burstow , Surrey.
Edmond Halley geboren am 29. Oktober in Haggerston bei London und gestorben am 14. Januar 1741 in Greenwich.
James Bradley geboren
am 3. März 1693 in Sherborne, Gloucestershire und
gestorben am 13. Juli 1762 in Chalford.
Nathaniel Bliss geboren am 28. November 1700 in Bisley, Gloucestershire und gestorben am 2.September 1764 in Oxford
Nevil Maskelyne geboren am 6. Oktober 1732 in London und gestorben am 9. Februar 1811 in Greenwich
Der Fahrstrahl eines Planeten markiert in gleichen Zeitabschnitten Flächen mit identischem Flächeninhalt (zweites Keplersches Gesetz). Das impliziert aber das sich Objekte auf einer elliptischen Umlaufbahn immer unterschiedlich schnell bewegen. Im Bereich der Apoapsis bewegen sich die Objekte am langsamsten und im Bereich der Periapsis am schnellsten.
The ray of a planet marks surfaces with identical area content in the same time periods (second Kepler's law). However, this implies that objects in an elliptical orbit always move at different speed. In the area of apoapsis, the objects move the slowest and in the periapsis area the fastest.
Die Flächeninhalte der roten und blauen Segmente sind identisch. Aber die Bahnlänge ist im roten Segment deutlich länger als beim blauen Segment. Somit bewegen sich Objekte unterschiedlich schnell.
The area contents of the red and blue segments are identical. But the web length is significantly longer in the red segment than in the blue segment. Thus, objects move at different speed.
Der Fahrstrahl eines Planeten simuliert mit Geogebra. Die Simulation läuft mit konstanter Geschwindigkeit ab und somit ergeben sich für gleiche Bahnlängen unterschiedliche Flächeninhalte der Segmente. (Umkehrschluss Kepler Gesetz 2)
The ray of a planet simulates with geogebra. The simulation runs at a constant speed and thus results in different area contents of the segments for equal web lengths. (Inverse Kepler Law 2)
Die synodische (Bezogen auf einen Beobachter auf der Erde) Umlaufzeit beträgt im Mittelwert 29 Tage 12 Stunden 44 Minuten 2.88… Sekunden. Aber dies ist eben nur der Mittelwert. Eine Lunation kann bis zu ±6 Stunden variieren und es kommt noch schlimmer, die Abweichungen sind nicht gleichmässig, sondern addieren oder subtrahieren sich laufend zu einem Maximum oder Minimum. Die untenstehende Grafik zeigt diese Funktion die aus 113 Vollmondlunationen besteht.
The synodic (relative to an observer on Earth) orbital period is an average of 29 days 12 hours 44 minutes 2.88... Seconds. But this is just the average. A Lunation can vary up to ±6 hours and it gets worse, the deviations are not uniform, but add up or subtract continuously to a maximum or minimum. The graphic below shows this function consisting of 113 full moon Lunations.
In der X-Achse sind die Lunationen eingetragen. Die Y-Achse zeigt die Lunationsdauer an.
Manche Lunationen sind nahe am Mittelwert (Rote Linie), doch schon die nächstfolgende kann drei Stunden früher oder später eintreffen. Eine Sequenz besteht immer aus 8 Wellenbergen und umfasst zwischen 111 und 113 Lunationen. Wie kommt eine solche “Schwebung” zustande ? Zu erkennen sind verschiedene Zyklen. Zum einen sehen wir einen Zyklus von knapp 13 Lunationen, das entspricht ca. einem Jahr. Somit ist in dieser Funktion der Erdumlauf um die Sonne enthalten. Zum anderen steigen die Amplituden der Funktion stetig an bis zu einem Maximum und nehmen danach wieder stetig ab. Dieser Zyklus dauert ca. 9 Jahre und hängt mit der Drehung des Apsidenlinie der Mondbahn zusammen.
DIE MONDPHASEN / MOONPHASES
Die Darstellung der Mondphasen bei den meisten Armbanduhren entspricht nicht der tatsächlich beobachtbaren Realität. In den meisten Komplikationen wird die Mondphase als Schnittmenge zweier Kreise die ineinander verschoben werden dargestellt.
The mechanical representation of the moon phases does not correspond to the actual observable reality. In most complications, the moon phase is represented as an intersection of two circles that are moved into each other.
Die Scheibe B hat in der Abbildung rechts bereits 40° zurückgelegt, bedeckt aber nur 28.2 % der Mondoberfläche (schraffierte Fläche). Der Drehwinkel von Scheibe B und die abgedeckte Fläche sind also nicht als Lineare Abbildung darstellbar. Die Berechnung der abgedeckten Fläche kann Trigonometrisch oder Algebraisch mit einer Polynomgleichung dritten Grades erfolgen.
The disk B has already moved 40° in the figure on the right, but covers only 28.2% of the lunar surface (hatched surface). The angle of rotation of disk B and the covered surface are therefore not representable as linear Equation. The calculation of the covered area can be done by a trigonometric or algebraic solution
Herleitung der Trigonometrischen Lösung. Der Rotationswinkel d (Delta) gelb markiert, entspricht dem Drehwinkel der Mondphasenscheibe auf einer Uhr.
Derivation of the trigonometric solution. The rotation angle d (delta) marked yellow corresponds to the rotation angle of the moon phase disk on a clock.
Durch ein Polynom dritten Grades kann die Funktion schon sehr genau abgebildet werden. Der Fehler liegt unter einem Prozent. Das x entspricht dem Rotationswinkel d (Delta).
Due to a third-degree polynomial, the function can already be mapped very precisely. The error is less than one percent. The x corresponds to the rotation angle d (delta).
Anhand des Graphen wird deutlich das es sich sicher nicht um eine Lineare Funktion handelt. Die Anzeige der Mondphase einer Uhr stimmt erst bei einem Rotationswinkel von ca. 60° ungefähr mit der tatsächlichen Mondphase überein. Lösen kann man dieses “Problem” durch Indexe auf dem Zifferblatt , oder mit einem Differenzial das die Mondphasenscheibe oder den Mond antreibt.
The graph makes it clear that it is certainly not a linear function. The display of the moon phase of a clock only approximates the actual moon phase at a rotation angle of about 60°. This "problem" can be solved by indexes on the dial, or with a differential that drives the moon phase disk or the moon.
ZAHNRAD-BERECHNUNGEN / GEARCALCULATION
Im Gegensatz zur typischen Uhrmacherkunst die früher fast ausschliesslich Zykloide und Hypozykloide Verzahnungen verwendeten (infolge geringerer Reibung bei einem Antrieb vom langsamen ins schnelle) haben die Zahnräder des Telluriums eine Evolventen Verzahnung. Diese bietet bei dieser Verwendung nur Vorteile. Die Evolventen Verzahnung hat eine Gerade als Eingriffslinie. Die Eingriffslinie schneidet die Tangente im Wälzpunkt in einem rechten Winkel. Sie ist also zugleich Berührungsnormale. Die Eingriffslinie tangiert ebenfalls die beiden Grundkreise der Räder. Beim Umkehren der Drehrichtung ändert sich die Eingriffslinie spiegelbildlich. Die Krümmung der Zahnflanken ρ (rho) sind im jeweiligen Berührpunkt Unterschiedlich gross, ihre Summe jedoch bleibt konstant. Die Zahnflanken wälzen sich nicht nur aufeinander ab, sondern Gleiten auch.
In contrast to the typical watchmaking art, which used to use almost exclusively cycloid and hypocycloid gearing (due to lower friction in a drive from slow to fast), the gears of the tellurium have a evolvenent gearing. This only offers advantages in this use. The Evolventen toothing has a straight line as an intervention line. The intervention line intersects the tangent at a right angle at the rolling point. It is therefore at the same time a normal of contact. The intervention line also affects the two basic circuits of the wheels. When the direction of rotation is reversed, the line of intervention changes in a mirror image. The curvature of the tooth flanks (rho) are different in the respective touch point, but their sum remains constant. The tooth flanks not only roll off on each other, but also glide.
Die Flankenpunkte A1 und A2 kommen in A zur Berührung, die Flankenpunkte B1 und B2 in B. Demzufolge arbeitet in diesem Abschnitt der Flankenteil A1B1 mit dem Flankenteil A2B2 zusammen. Da beide verschieden lang sind, kennzeichnet die Längendifferenz den Gleitweg. Der kürzere Flankenteil wird stärker abgenützt. Die Gleitgeschwindigkeit vg ist die Differenz der beiden Tangential-geschwindigkeiten vt1 und vt2, und zwar vg = vt1 – vt2 für Flankenpunkte an MGZ1, vg = vt2 – vt1 für Flankenpunkte an MGZ2. Unter spezifischem Gleiten versteht man also das Maß für das Gleiten der Zahnflanken und somit das Verhältnis der Gleitgeschwindigkeit zur Tangentialgeschwindigkeit des jeweiligen Berührpunktes der entsprechenden Flanke. Im Wälzpunkt ist die Differenz der beiden Tangentialgeschwindigkeiten gleich null und somit findet dort kein Gleiten statt.
The flank points A1 and A2 come into contact in A, the flank points B1 and B2 in B. Consequently, in this section of the flank part A1B1 cooperates with the flank part A2B2. Since both are different in length, the length difference indicates the sliding path. The shorter flank part is worn out more heavily. The sliding velocity vg is the difference between the two tangential speeds vt1 and vt2, namely vg = vt1 – vt2 for flank points at MGZ1, vg = vt2 – vt1 for flank points at MGZ2. By specific gliding one means the measure for the sliding of the tooth flanks and thus the ratio of the sliding velocity to the tangential velocity of the respective touch point of the corresponding flank. In the rolling point, the difference between the two tangential velos is zero and therefore no sliding takes place there.
Für die Berechnungen des spezifischen Gleitens wurden die unten aufgeführten Formeln verwendet. Alle Zahnflanken wurden ohne eine Profilverschiebung hergestellt. Die Berechnung wurde nicht nur für einen einzelnen Punkt der Eingriffsstrecke gerechnet, sondern für den ganzen Eingriffsbereich.
The formulas listed below were used for the calculations of the specific slide. All tooth flanks were manufactured without a profile shift. The calculation was calculated not only for a single point of the course of the procedure, but for the entire scope of the procedure.
Das Verhältnis der Zähnezahl z2 des Grossrades zur Zähnezahl z1 des Kleinrades ist das Zähnezahl Verhältnis u. Das unten stehende Berechnungsbeispiel zeigt die Werte der spezifischen Gleitung am Punkt 3.82 mm der Eingriffslinie des Zahnradpaares MGZ_1 und MGZ_2.
The ratio of the number of teeth z2 of the large wheel to the number of teeth z1 of the small wheel is the number of teeth ratio u. The calculation example below shows the values of the specific glider at point 3.82 mm of the gear pair's intervention line MGZ_1 and MGZ_2.
Die Berechnung der spezifischen Gleitung aller Zahnradpaare wurde mit EXCEL realisiert. Hier
wurde der ganze Bereich der Eingriffslinie berücksichtigt. Wobei zu erwähnen bleibt dass zur Erzeugung der Funktion ein Inkrement von 0.05 mm gewählt wurde. Die Funktion des spezifischen Gleitens kann mit einer Polynomfunktion sechsten Grades schon sehr genau angenähert werden.
The calculation of the specific gdirect of all gear pairs was realized with EXCEL. Here, the whole area of the intervention line was taken into account. It should be noted that an increment of 0.05 mm was chosen to generate the function. The function of the specific gliding can be approximated with a sixth degree polynomial function.
EMAILLIEREN / ENAMEL
Per Definition ist Email ein Überzug von Glasschmelz auf Metall. Bereits die alten Ägypter kannten dieses Glasschmelzverfahren und wendeten es vorwiegend für die Schmuckherstellung an. In Europa wurden die ersten Emaillarbeiten von den Kelten ca. 500 Jahre v. Chr. erschaffen. Das sogenannte "Blutemail" war von roter Farbe und wurde auf Gebrauchsgegenstände aufgeschmolzen. Auch Schmuck wurde damit verziert.
By definition, email is a coating of glass melt to metal. Already the ancient Egyptians knew this glass melting process and used it mainly for jewelry production. In Europe, the first enamel works were created by the Celts about 500 years BC. The so-called "blood e-mail" was of red color and was melted on utensils. Jewellery was also decorated with it.
Entstanden ist das Email oder Emaillieren ohne Zweifel aus der Kunst, keramische und glasige Werkstoffe zu schmelzen und kunstgewerblich zu verwenden. Es gibt viele unterschiedliche Techniken des Emaillierens, jedoch sind die bekanntesten sicher das "émail champlevé" oder Grubenschmelz, das "émail cloisonné" oder Zellenschmelz, das "émail à jour" oder Fensteremail und die Emailmalerei, die als "Königsdisziplin" des Emaillierens gilt.
The result is enamelling from the art of melting ceramic and glassy materials and using them for the arts. There are many different techniques of enamelling, but the most well-known are certainly the "émail champlevé" or mine melt, the "émail cloisonné" or cell melt, the "émail jour" or window e-mail and the enamel painting, which is considered "the "king discipline" of enamel.
In einem meiner Projekte brachte ich die vier Jahreszeiten von Giuseppe Arcimboldo (1526-1593) mittels Emailmalerei auf Metallplättchen auf. Die Plättchen haben eine Grösse von 41 x 30 mm im Gegensatz zu den Originalen im Louvre die auf Holztafeln der Grösse 66 x 50 cm gemalt wurden.
In one of my projects, I applied the four seasons of Giuseppe Arcimboldo (1526-1593) to metal plates using enamel painting. The plates have a size of 41 x 30 mm in contrast to the originals in the Louvre, which were painted on wooden panels of the size 66 x 50 cm.
FRÜHLING / SPRING
Original von Giuseppe Arcimboldo (* um 1526 in Mailand; † 11. Juli 1593)
SOMMER / SUMMER
Original von Giuseppe Arcimboldo (* um 1526 in Mailand; † 11. Juli 1593)
HERBST / AUTUMN
Original von Giuseppe Arcimboldo (* um 1526 in Mailand; † 11. Juli 1593)
WINTER / WINTER
Original von Giuseppe Arcimboldo (* um 1526 in Mailand; † 11. Juli 1593)
Es gibt verschiedene Möglichkeiten eine Mondphasenanzeige dar zu stellen. Bei der “Perpetual Moon” habe ich mich für einen statischen Mond entschieden, der durch eine dynamische Phasenscheibe abgedeckt respektive aufgedeckt wird. Der Mond hat einen Durchmesser von 13 mm und gehört somit zu den grössten die jemals auf einer Armbanduhr platz fanden. Die ungeschliffene Emaillierte Mondscheibe hat eine Dicke von max. 0.4 mm und wirkt durch die Unebenheiten die beim Brennen entstehen sehr plastisch. Der Betrachter hat das Gefühl einen dreidimensionalen Körper vor sich zu haben.
There are several ways to display a moon phase display. In the "Perpetual Moon" I decided on a static moon, which is covered or revealed by a dynamic phase disk. The moon has a diameter of 13 mm, making it one of the largest ever to be placed on a wristwatch. The unpolished enamelled lunar disc has a thickness of max. 0.4 mm and has a very plastic effect due to the unevenness caused by burning. The viewer has the feeling of having a three-dimensional body in front of him.
Die Herstellung des Mondes umfasst mehrere Herstellungsschritte und die grösste Herausforderung besteht darin, das die nur 0.20 mm dicken Silberplättchen nach dem Brennen bei fast 1000° C flach bleiben.
The production of the moon involves several manufacturing steps and the biggest challenge is that the silver plates, which are only 0.20 mm thick, remain flat at almost 1000° C after burning.
Schritt 3. Aufbringen der verschiedenen Emails und Brennen bei 930°C.
Schritt 5. Ausarbeiten der Mondstrukturen (Marias)
Wie schon mit blossem Auge von der Erde aus sichtbar ist, hat der Mond charakteristische Strukturen auf seiner Oberfläche. Das “Mare Imbrium”, “Mare Serenitatis”, “Mare Tranquilitatis” und das “Mare Crisium” sind fast jederzeit erkennbar.
As can be seen from Earth with a naked eye, the moon has characteristic structures on its surface. The "Mare Imbrium", "Mare Serenitatis", "Mare Tranquilitatis" and the "Mare Crisium" are almost always recognizable.
Eine wunderschöne Aufnahme des “Mare Imbrium” (Meer des Regens) mit meinem Teleskop. Sehr gut zu erkennen sind die Krater “Archimedes, Aristillus und Autolycus” die ein Dreieck bilden, sowie an der Erdschattengrenze der Krater “Plato” der einen Durchmesser von 101 km und einer tiefe von 1000 m. Der Kraterwall erhebt sich bis zu 2400 m.
A beautiful shot of the "Mare Imbrium" (Sea of Rain) with my telescope. Very clearly visible are the craters "Archimedes, Aristillus and Autolycus", which form a triangle, as well as at the earth's shadow boundary the crater "Plato" of a diameter of 101 km and a depth of 1000 m. The crater wall rises up to 2400 m.
GUILLOCHIEREN / GUILLOCHING
Papiergeld gibt es in Europa seit dem14. Jahrhundert. Um Fälschungen vorzubeugen entstanden mit der Zeit verschiedene Verfahren, um Papiergeld fälschungssicher zu machen. Das Guillochieren ist eine halbautomatische Graviertechnik und entstand im 16. Jahrhundert und wurde als erstes für das Gravieren von Druckplatten für die Geldnoten und Wertpapier Herstellung eingesetzt. Im 18. Jahrhundert wurde die Technik von den Uhrmachern aufgenommen um Taschenuhren zu verzieren. Um ca. 1930 wurde das Guillochieren durch andere (automatische) Gravierverfahren ersetzt, da die produzierten Stückzahlen stark anstiegen und fast keine Taschenuhren mehr produziert wurden. Das traditionelle Guillochieren wird mit handbetriebenen Maschinen ausgeführt, man unterscheidet hier sogenannte Rundzug und Geradezug Maschinen. Guillochiermuster entstehen also durch die Überlagerung mindestens zweier Bewegungen (Achsen). Während der Guillochierbewegung wird ein Stichel von Hand gegen das Werkstück gedrückt. Die meisten noch vorhandenen Maschinen stammen aus dem 19. Jahrhundert oder sogar aus dem 18. Jahrhundert.
Paper money has been available in Europe since 14. Century. In order to prevent counterfeiting, various methods were developed over time to make paper money counterfeit-proof. Guilloching is a semi-automatic engraving technique that originated in the 16th century and was first used for engraving printing plates for banknotes and securities production. In the 18th century, the technique was taken up by the watchmakers to decorate pocket watches. Around about 1930, guilloching was replaced by other (automatic) engraving methods, as the quantities produced increased sharply and almost no pocket watches were produced. Traditional guilloching is carried out with hand-operated machines, so-called round and straight-line machines. Guillochier patterns are thus created by the overlay of at least two movements (axes). During the Guillochier movement, a stitch is pressed by hand against the workpiece. Most of the machines still available date back to the 19th century or even from the 18th century.
Original Guillochiermaschinen aus der Zeit zwischen dem 18. und 19. Jahrhundert sind heute sehr begehrte Objekte. Wer eine hat gibt sie ganz bestimmt nicht her. Steht eine zum Verkauf ist der Preis derart hoch dass Sie für eine Privatperson unerschwinglich ist. Somit musste ich für meine Guillochierarbeiten selbst eine bauen.
Original Guillochier machines from the period between the 18th and 19th centuries are today highly sought-after objects. Whoever has one certainly does not give it. If one is for sale, the price is so high that it is unaffordable for a private person. So I had to build one myself for my guilloching works.
Um die Deckplatte der “Perpetual Moon” guillochieren zu können konstruierte ich eine Guillochier Vorrichtung zu meiner Schaublin 102. Der Antrieb erfolgt mit traditioneller Handkurbel. Die Schablone mit Zustellmechanismus ist an der Hauptspindel vorne angebracht.
In order to Guilloche the cover plate of the "Perpetual Moon" I constructed a guillochier device to my Schaublin 102. The drive is carried out with a traditional hand crank. The template with delivery mechanism is attached to the main spindle at the front.
Bewegungsablauf beim Guillochieren. Theoretisch kann man mit nur einer einzigen Schablone unendlich viele verschiedene Muster erzeugen.
Movement sequence during guilloching. Theoretically, you can create an infinite number of different patterns with just one stencil.
Detailaufnahme durch das Mikroskop hindurch. Schön zu sehen ist der Span der durch den Stichel heraus “Guillochiert” wird.
Detailed view through the microscope. Beautiful to see is the shavings that is "guilloched" by the steel.
ZAHNRAD PERMUTATIONEN / GEAR PERMUTATIONS
Wenn ein Übersetzungsverhältnis mit Zahnrädern dargestellt werden muss, sollten vorab einige Randbedingungen definiert sein. Die Anzahl der zu verwendenden Zahnräder oder die maximale Anzahl der Zähne pro Zahnrad sind solche Randbedingungen. Infolge der Reibung sollte die Anzahl der im Eingriff stehenden Zahnräder minimal gehalten werden.
If a gear gear ratio needs to be represented, some boundary conditions should be defined in advance. The number of gears to be used or the maximum number of teeth per gear are such boundary conditions. As a result of friction, the number of gears in intervention should be kept to a minimum.
Ein Übersetzungsverhältnis ist definiert durch den Quotienten der treibenden und der getriebenen Zahnräder. Sofort erkennen wir dass sich ein Übersetzungsverhältnis aus zwei Produkten in einem Quotienten zusammensetzt. Diese Produkte wiederum bestehen aus Faktoren. Um das Übersetzungsverhältnis möglichst genau darstellen zu können, besteht die
Aufgabe darin, geeignete Faktoren zu suchen die dieses Verhältnis abbilden.
A gear ratio is defined by the quotient of the driving and the driven gears. We immediately realize that a translation ratio of two products is composed in one quotient. These products, in turn, consist of factors. In order to be able to present the translation ratio as accurately as possible, the task is to look for suitable factors that represent this ratio.
Liegt das gesuchte Verhältnis in ℕ wird man vermutlich sehr schnell geeignete Faktoren finden, da die Zähnezahlen ebenfalls in ℕ liegen. Schwieriger wird es wenn man Verhältnisse Abbilden will die in ℝ liegen. Die synodische Umlaufzeit des Mondes um die Erde beträgt 29.53059
Tage, somit darstellbar als Verhältnis von 1 : 29.53059. Ein möglicher Ansatz wäre es die beiden Zahlen zu erweitern, nämlich zu 100`000 : 2`953`059 und eine Primfaktorenzerlegung
anzuwenden. Jedoch lässt sich 2`953`059 nur in 3 * 984`353 zerlegen und 100`000
ist bestimmt nicht durch drei teilbar in ℕ.
If the desired ratio is in N, one will probably find suitable factors very quickly, since the number of teeth is also in N. It becomes more difficult if you want to map conditions that lie in R. The synodic orbital period of the moon around the earth is 29.53059 days, thus representable as a ratio of 1: 29.53059. One possible approach would be to extend the two figures, namely to apply 100'000 : 2'953'059 and a prime factor decomposition. However, 2'953'059 can only be broken down into 3 * 984'353 and 100'000 is certainly not divisible by three in N.
Wir müssen einen Algorithmus finden mit dem man beliebige Verhältnisse möglichst genau annähern kann. Betrachten wir zunächst einmal zwei Zahnräder z1 und z2 die unterschiedliche Zähnezahlen besitzen, nämlich zz1 = 10 und zz2 = 11. Die mögliche Anzahl an Anordnungen sogenannte Permutationen sehen wir in der Tabelle. Bei zwei Zahnrädern mit unterschiedlichen Zähnezahlen n=2 gibt es 3 Möglichkeiten diese Anzuordnen.
We have to find an algorithm with which you can approximate any ratio as accurately as possible. First, consider two gears z1 and z2 that have different number of teeth, namely zz1 = 10 and zz2 = 11. The possible number of arrangements of so-called permutations can be seen in the table. With two gears with different number of teeth n=2 there are 3 ways to arrange these.
Wird die Zähnezahl n der zwei Zahnräder um eins erhöht, haben wir bereits 6 Permutationen. Wir setzen diese Reihe fort und Füllen die erhaltenen Werte in eine Tabelle ein.
If the number of teeth n of the two gears is increased by one, we already have 6 permutations. We continue this series and fill the obtained values into a table.
Als nächstes wiederholen wir diese ganzen Berechnungen mit einem zusätzlichen Zahnrad z3 die wieder unterschiedliche Zähnezahlen haben können. Somit haben wir jetzt drei Zahnräder z1, z2 und z3. Die mögliche Anzahl an Permutationen bei drei Zahnrädern mit unterschiedlichen Zähnezahlen n=2 ist 4.
Next, we repeat all these calculations with an additional gear z3, which can again have different number of teeth. So we now have three gears z1, z2 and z3. The possible number of permutations in three gears with different number of teeth n=2 is 4.
Wird die Zähnezahl n der drei Zahnräder um eins erhöht, haben wir bereits 10 Permutationen. Wir setzen diese Reihe fort und Füllen die erhaltenen Werte in eine Tabelle ein.
If the number of teeth n of the three gears is increased by one, we already have 10 permtations. We continue this series and fill the obtained values into a table.
Die Berechnungen können so in dieser Form beliebig fortgesetzt werden. Wir stellen die bisher erhaltenen Resultate tabellarisch zusammen und zeigen auf wie sich diese Folge entwickelt.
The calculations can thus be continued as desired in this form. We put together the results obtained so far in tabular form and show how this episode develops.
Somit gilt für ni Zahnräder
Thus, for ni gears
Dabei gibt ni die Anzahl der verwendeten Zahnräder an und die Größe von n1 gibt an die Differenz der maximalen Zähnezahl minus die minimale Zähnezahl der Zahnräder. Mit dieser Formel berechnet man die Anzahl von Produkten die entstehen wenn man mehrere Zahnräder mit unterschiedlichen Zähnezahlen kombinieren will. Sie dient als Basis für einen Algorithmus zur Berechnung von Übersetzungsverhältnissen. Mithilfe dieser Berechnungsformel wird sichergestellt, dass nur Produkte für die Berechnung verwendet werden deren Faktoren in ℕ sind und die sich in einer Permutationsgruppe befinden und somit eindeutig faktorisierbar sind.
Here ni indicates the number of gears used and the size of n1 indicates the difference of the maximum number of teeth minus the minimum number of teeth of the gears. This formula calculates the number of products that arise when you want to combine several gears with different numbers of teeth. It serves as the basis for an algorithm for calculating translation ratios. This calculation formula ensures that only products are used for the calculation whose factors are in N and that are in a permutation group and are therefore clearly factorizable.