Die Umlaufbahn des Mondes um die Erde entspricht einer Ellipse mit einer numerischen Exzentrizität von 0.055545. Während in der Mathematik die Exzentrizität einer Ellipse mit der Distanz zwischen einem der beiden Brennpunkte (F1, F2) und dem Mittelpunkt M definiert ist (e = lineare Exzentrizität), gilt in der Astronomie für die Beschreibung eines Orbits die numerische Exzentrizität E. E ist definiert durch den Quotienten e/a, also lineare Exzentrizität dividiert durch die grosse Halbachse a. Die Exzentrizität beschreibt also die Abweichung einer Ellipse von einem Kreis.
The orbit of the moon around the Earth corresponds to an ellipse with a numerical eccentricity of 0.055545. While in mathematics the eccentricity of an ellipse is defined with the distance between one of the two focal points (F1, F2) and the center M (e = linear eccentricity), in astronomy the numerical eccentricity E. E is defined by the quotient E/a, i.e. linear eccentricity divided by the large half axis a. The eccentricity thus describes the deviation of an ellipse from a circle.
Mit einer numerischen Exzentrizität von 0.055545 beschreibt die Mondbahn fast eine Kreisbahn um die Erde, aber eben nur fast. In einem der beiden Brennpunkte (F1, F2) einer Ellipse befindet sich der Zentralkörper (Erde). Durch die Gravitationseinwirkung der Erde umkreist der Mond dieselbe. Das gemeinsame Rotationszentrum befindet sich nicht wie erwartet im Erdmittelpunkt, sondern im sogenannten Baryzentrum dem gemeinsamen Schwerpunkt ca. 1700 km unterhalb des sublunaren Punktes im Erdmantel.
With a numerical eccentricity of 0.055545, the lunar orbit describes almost a circular orbit around the Earth, but only almost. In one of the two focal points (F1, F2) of an ellipse is the central body (earth). Due to the gravitational effect of the Earth, the moon orbits the same. The common rotation center is not located in the center of the earth as expected, but in the so-called bary center of the common center of gravity about 1700 km below the sublunar point in the earth's mantle.
Da die Mondbahn eine Ellipse beschreibt, ist seine Distanz zur Erde variabel. Das Apogäum ist im Mittel 405`504 km von der Erde entfernt, das Perigäum im Mittel 363`296 km. Die Verbindung von Apogäum und Perigäum nennt man Apsidenlinie oder Apsis. Die Apoapsis ist also der Scheitel mit der grössten Entfernung und die Periapsis der Scheitel mit der kleinsten Entfernung zum Zentralkörper.
Since the lunar orbit describes an ellipse, its distance from Earth is variable. The Apogäum is on average 405'504 km from the earth, the perigee on average 363'296 km. The combination of apogee and perigee is called an apse line or apse. The apoapsis is thus the apex with the greatest distance and the periapsis of the apex with the smallest distance to the central body.
Die Apsiden erhalten unterschiedliche Bezeichnungen bezüglich ihres Zentralkörpers. So zum Beispiel
Sonne = Aphel und Perihel (hel = Helios die Sonne)
Erde = Apogäum und Perigäum (gäum = Gaia die Erde)
Mars = Apares und Periares (ares =Mars)
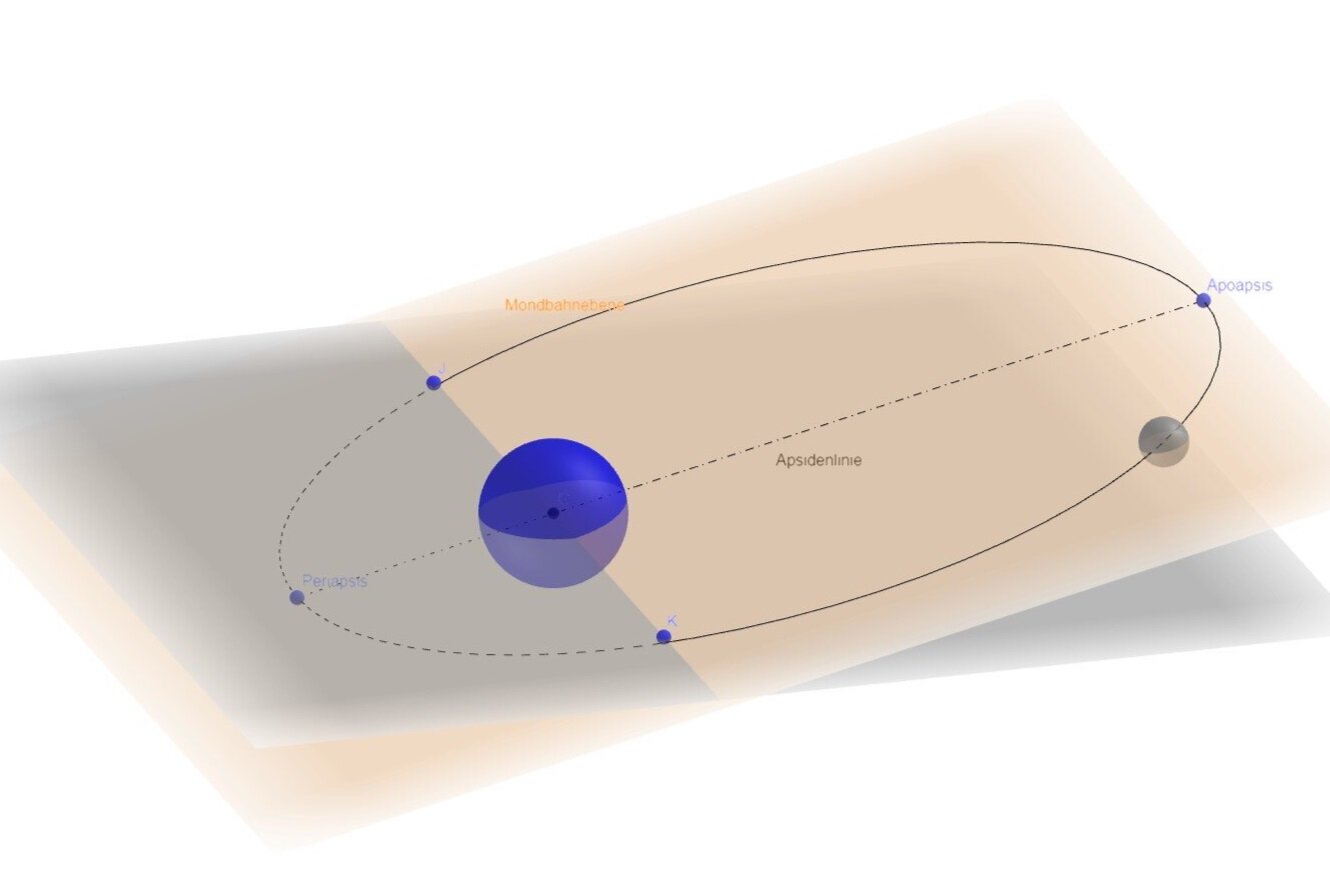
Die grau gefärbte Ebene markiert die Ekliptik, also die Ebene auf der die Erde die Sonne umkreist. Die braun eingefärbte Ebene, ist die Ebene der Mondbahn, sie ist im mittel 5.14527° gegenüber der Ekliptik geneigt. Die beiden Punkte J,K markieren die Stellen wo der Mond die Ekliptik ebene schneidet, die sogenannten Knoten (Drachenpunkte). Die Verbindung der beiden Punkte heisst Knotenlinie. Die Zeitdauer die der Mond benötigt um durch den gleichen Knoten zu wandern wird als “Drakonitischer Monat” bezeichnet und Dauert im mittel 27.212221 Tage. Mond oder Sonnenfinsternisse sind nur in der Nähe der beiden Knoten möglich und auch immer nur bei gleichzeitigem Vollmond oder Neumond. Die Knoten sind nicht fix im Raum sondern verschieben sich retrograd um ca. 19.3° pro Jahr.
The gray-colored plane marks the ecliptic, the plane on which the Earth orbits the sun. The brown colored plane, is the plane of the lunar orbit, it is inclined in the mean 5.14527° opposite the ecliptic. The two points J,K mark the places where the moon intersects the ecliptic plane, the so-called nodes (dragon points). The connection of the two points is called node line. The time it takes for the moon to travel through the same node is called the "Drakonite Month" and lasts in the middle of 27.212221 days. Moon or solar eclipses are only possible near the two knots and only at the same time full moon or new moon. The knots are not fixed in space but shift retrograde by about 19.3° per year.
Simulation in GEOGEBRA zur Berechnung der Drachenpunkte. Distanzen und Geschwindigkeiten entsprechen nicht der Realität.
Simulation in GEOGEBRA to calculate the dragon points. Distances and speeds do not correspond to reality.
Die meisten Grundlagen wurden bereits im 16. - 19. Jahrhundert erarbeitet. Anlässlich meines Besuches in der Sternwarte von Greenwich im Jahre 2016 war ich auf den Spuren der ersten “Himmelsmechaniker”. Es sind Namen wie Kepler, Kopernikus, Bradley, Newton und Halley die die Himmelsmechanik revolutionierten.
Most of the foundations were already worked out in the 16th - 19th century. On the occasion of my visit to the Greenwich Observatory in 2016, I was following in the footsteps of the first "heavenly mechanics". They are names like Kepler, Copernicus, Bradley, Newton and Halley that revolutionized celestial mechanics.
John Flamsteed geboren am 19. August 1646 Denby , Derbyshire und gestorben am 31. Dezember 1719 Burstow , Surrey.
Edmond Halley geboren am 29. Oktober in Haggerston bei London und gestorben am 14. Januar 1741 in Greenwich.
James Bradley geboren
am 3. März 1693 in Sherborne, Gloucestershire und
gestorben am 13. Juli 1762 in Chalford.
Nathaniel Bliss geboren am 28. November 1700 in Bisley, Gloucestershire und gestorben am 2.September 1764 in Oxford
Nevil Maskelyne geboren am 6. Oktober 1732 in London und gestorben am 9. Februar 1811 in Greenwich
Der Fahrstrahl eines Planeten markiert in gleichen Zeitabschnitten Flächen mit identischem Flächeninhalt (zweites Keplersches Gesetz). Das impliziert aber das sich Objekte auf einer elliptischen Umlaufbahn immer unterschiedlich schnell bewegen. Im Bereich der Apoapsis bewegen sich die Objekte am langsamsten und im Bereich der Periapsis am schnellsten.
The ray of a planet marks surfaces with identical area content in the same time periods (second Kepler's law). However, this implies that objects in an elliptical orbit always move at different speed. In the area of apoapsis, the objects move the slowest and in the periapsis area the fastest.
Die Flächeninhalte der roten und blauen Segmente sind identisch. Aber die Bahnlänge ist im roten Segment deutlich länger als beim blauen Segment. Somit bewegen sich Objekte unterschiedlich schnell.
The area contents of the red and blue segments are identical. But the web length is significantly longer in the red segment than in the blue segment. Thus, objects move at different speed.
Der Fahrstrahl eines Planeten simuliert mit Geogebra. Die Simulation läuft mit konstanter Geschwindigkeit ab und somit ergeben sich für gleiche Bahnlängen unterschiedliche Flächeninhalte der Segmente. (Umkehrschluss Kepler Gesetz 2)
The ray of a planet simulates with geogebra. The simulation runs at a constant speed and thus results in different area contents of the segments for equal web lengths. (Inverse Kepler Law 2)
Die synodische (Bezogen auf einen Beobachter auf der Erde) Umlaufzeit beträgt im Mittelwert 29 Tage 12 Stunden 44 Minuten 2.88… Sekunden. Aber dies ist eben nur der Mittelwert. Eine Lunation kann bis zu ±6 Stunden variieren und es kommt noch schlimmer, die Abweichungen sind nicht gleichmässig, sondern addieren oder subtrahieren sich laufend zu einem Maximum oder Minimum. Die untenstehende Grafik zeigt diese Funktion die aus 113 Vollmondlunationen besteht.
The synodic (relative to an observer on Earth) orbital period is an average of 29 days 12 hours 44 minutes 2.88... Seconds. But this is just the average. A Lunation can vary up to ±6 hours and it gets worse, the deviations are not uniform, but add up or subtract continuously to a maximum or minimum. The graphic below shows this function consisting of 113 full moon Lunations.
In der X-Achse sind die Lunationen eingetragen. Die Y-Achse zeigt die Lunationsdauer an.
Manche Lunationen sind nahe am Mittelwert (Rote Linie), doch schon die nächstfolgende kann drei Stunden früher oder später eintreffen. Eine Sequenz besteht immer aus 8 Wellenbergen und umfasst zwischen 111 und 113 Lunationen. Wie kommt eine solche “Schwebung” zustande ? Zu erkennen sind verschiedene Zyklen. Zum einen sehen wir einen Zyklus von knapp 13 Lunationen, das entspricht ca. einem Jahr. Somit ist in dieser Funktion der Erdumlauf um die Sonne enthalten. Zum anderen steigen die Amplituden der Funktion stetig an bis zu einem Maximum und nehmen danach wieder stetig ab. Dieser Zyklus dauert ca. 9 Jahre und hängt mit der Drehung des Apsidenlinie der Mondbahn zusammen.